Элементарная теория

	ATTENTION! THIS IS THE FIRST SKETCHES! ARTICLE WILL BE COMPLETED!
	ВНИМАНИЕ! ЭТО ПЕРВЫЕ ШТРИХИ! СТАТЬЯ БУДЕТ ЗАВЕРШЕНА!

Символы

Геометрическая логика оперирует четырьмя состояниями, которые мы будем именовать символами:

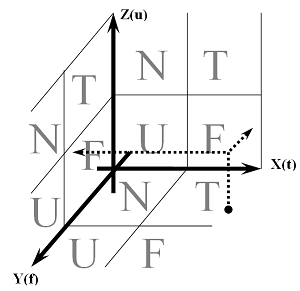
• N (от англ. “Null” ) - означает состояние «Вне понимания», геометрически в четырехмерном континууме интерпретируется, как координата оси времени -Ct.

• T (от англ. “True” ) – означает состояние «Правда», геометрически интерпретируется, как координата оси OХ, абсцисса.

• F (от англ. “False” ) - означает состояние «Ложь», геометрически интерпретируется, как координата оси OY, ордината.

• U (от англ. “Undefined” ) - означает состояние «Неопределенно», геометрически интерпретируется, как координата оси OZ, аппликата.

Направление обхода символов

Символы имеют прямой порядок следования N → T → F → U и обратный порядок следования U → F → T → N. Мы будем использовать прямой порядок следования символов для их нумерации: N=0 T=1 F=2 U=3 во всех наших построениях.

Мы можем использовать символы в качестве цифр и составлять из них числа в арифметике по основанию 4. Прямой порядок следования символов мы будем называть синтезирующим или индуктивным направлением обхода символов (0,1,2,3). Также такое направление будет называться по часовой стрелке или CW (от англ. clockwise) Обратный порядок следования символов - будем называть аналитическим или дедуктивным направлением обхода символов (3,2,1,0) и, соответственно, против часовой стрелки или CCW (от англ. counter clockwise).

на построениях символам часто также сопоставляются условные цвета в соответствии с длиной волны спектра N=0=красный    T=1= желтый     F=2= зеленый     U=3= синий .

Аксиомы

теперь, из определения символов и направлений их обхода возможно сформулировать две аксиомы

аксиома 1 Любой объект (логическое выражение) может находиться только в одном из 4-ех состояний по отношению к любому другому объекту:

• 1. данное выражение истинно (Т) (пример: белый цвет)
• 2. данное выражение ложно (F) (пример: черный цвет)
• 3. данное выражение неопределенно (U) (пример: серый цвет),
• 4. данное выражение бессмысленно, т.е. вне понимания (N) (пример: соленый цвет)

Указанные состояния являются дополняющими друг к другу и образуют полную группу состояний.

аксиома 2 Символы имеют прямой и обратный порядок следования.

Октаэдр

Возьмем некоторый произвольный объект X (например, некоторое слово из нашего языка). И некоторый второстепенный объект Y (опять, некоторое слово из нашего языка) и, дополнительно, этому объекту Y дадим второе название - свойство Y. В соответствии с аксиомой 1 высказывание «свойство Y присуще объекту Х» может находиться в одном из четырех (0,1,2,3) множеств эквивалентных объектов, каждое такое множество мы также будем считать объектом. Отобразим это графически:

свойство Y может находиться в одной из ячеек 0, 1, 2, 3.

Таким образом, свойство Y попадает в одно из множеств 0,1,2 либо 3. Обобщая наш пример, можно сказать, что абсолютно все свойства, которые только можно придумать или взять из речи: Y₀,Y₁,…,Y_n, по отношению к объекту X можно распределить по множествам эквивалентностей 0,1,2,3. Рассуждая далее – мы можем сказать, что "0","1","2" и "3" - это четыре объекта, которые определяют собой объект Х, в символах логики четырех состояний N,T,F,U. Раз это так, то по аналогии с объектом Х - каждый из объектов 0,1,2 и 3 имеет свои четыре группы свойств N,T,F,U. Причем для каждого из объектов 0,1,2,3 определена уже одно множество свойств через объект Х.

В дальнейшем, любые рассматриваемые объекты и их возможные (неспаренные) и существующие (спаренные) логические связи мы будем называть логическим построением. Изображение на рисунке является логическим построением:

логическое построение.

соединим соответствующие друг другу связи объекта "0" и объекта "1", потом
объекта "1" и объекта "2" , и далее
объекта "2" и объекта "3",
объекта "3" и объекта "0"
это можно сделать двумя способами и никак больше.

алгоритм октаэдр.

Алгоритм Октаэдр

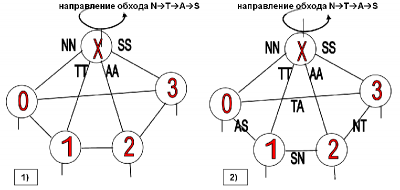
• 1. Соединим вспомогательные объекты между собой, как показано на рисунке в 1).
• 2. Зададим порядок обхода символов (например, прямой порядок N→T→F→U)
• 3. Определим значение связи 0—1, 1—2, 2—3 и 3—0 следующим образом:
• 3.1 для каждой связи вспомогательных объектов в качестве возможных остаются два символа. Укажем их в соответствии с выбранным порядком.
• 3.2 Например, связь 0—1 можно описать символами U или F и только ими

(символ N уже использован на построение связи 0—Х для объекта 0, аналогично символ T уже использован на построение связи 1—Х для объекта 1). т.к. мы задали прямой порядок N →T→F→U, то для связи 0—1 будем записывать последовательность FU (по заданному направлению обхода символов N→T→F→U сначала идет символ F, затем идет символ U)

• 4. В результате определения остальных связей (1-2, 2-3 и 3-0) получим 2) на рисунке

• 5. Опять рассмотрим объекты 0,1,2 и 3 и установим последовательности символов (комбинации) для оставшихся неопределенными связей 0—… , 1—… , 2—… и 3—… :
• 5.1. Для объекта 0, по первым символам всех уже установленных связей:

N, T, F – использованы. Свободен U.

• 5.2. Для объекта 0, по вторым символам: N, F, U – использованы. Свободен T.
• 5.3. В итоге Связь 0—… определена, как UT
• 6. Поступим аналогичным образом для связей: 1—… , 2—… и 3—… .
• 7. Объединим связи 0—… , 1—… , 2—… и 3—… . в объект Z.
• 8. Объект Z полностью определен в терминах логики четырех состояний и называется результирующим объектом. ( 3) и 4) на рисунке )

октаэдр. 3) - плоское представление; 4) - трехмерное представление.

Определения и свойства, связанные с октаэдром

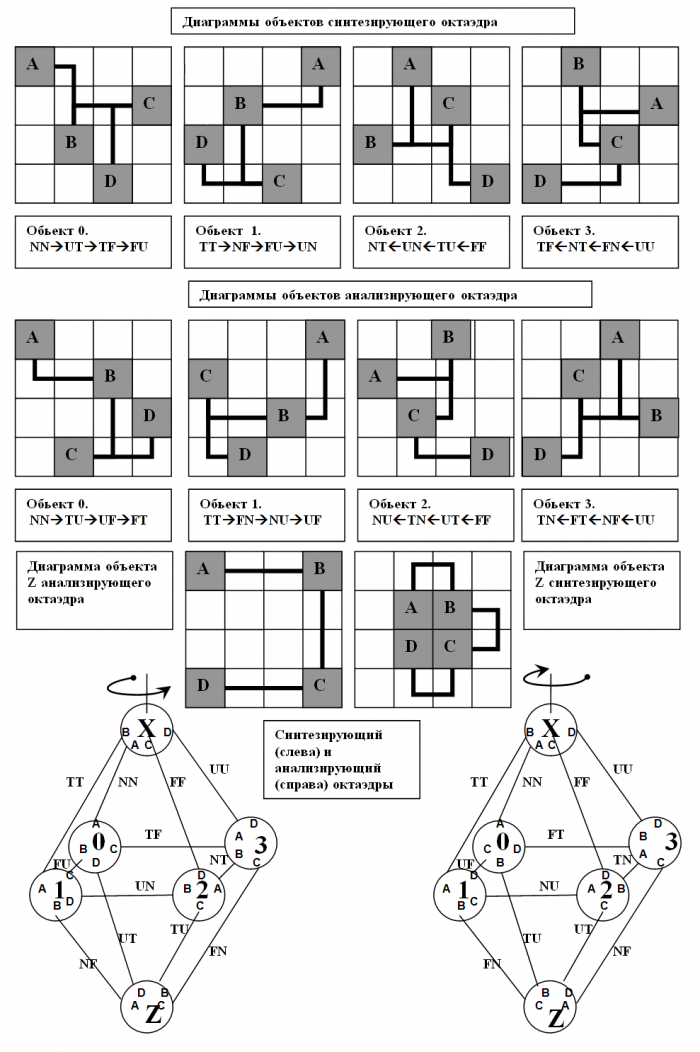
• 1. Полученное логическое построение является октаэдром. Октаэдр, распадается еще на 2 октаэдра. Связи первого, определяются по первому символу, а связи второго – по второму символу. Поэтому будем называть наше построение сдвоенным логическим октаэдром. Процесс, при котором определяется, каким из октаэдров является сдвоенный октаэдр, будем называть локализацией октаэдра.

Локализацией в общем смысле будем называть процесс выбора логического символа из некоторого набора допустимых символов (комбинации символов) для соотнесения его со связью. Сдвоенный октаэдр будем также называть нелокализованным логическим октаэдром, а каждое из построений изображенных на рисунке выше – локализованным логическим октаэдром.

• 2. Замечаем, что для построения локализованного октаэдра, необходимо задать 5 связей (4 связи исходного объекта X и одну из связей вспомогательных объектов). Если мы зададим только 4 связи, то получим нелокализованный октаэдр. Заметим также, что всего в октаэдре 12 связей.
• 3. Сдвоенный октаэдр на рисунке построен исходя из синтезирующего направления обхода символов N→T→F→U (прямой порядок). При построении нелокализованного октаэдра, исходя из аналитического направления обхода U→F→T→N (обратный порядок), все символы в двухсимвольных комбинациях ее связей поменяются местами. Воспользовавшись этим свойством, будем называть октаэдр, получающийся при локализации сдвоенного октаэдра по первым символам двухсимвольных комбинаций ее связей:

A) синтезирующим октаэдром (S - октаэдром), при условии, что сдвоенный октаэдр построен исходя из синтезирующего направления обхода символов N→T→F→U (левая часть рисунка). B) аналитическим октаэдром (A - октаэдром), при условии, что сдвоенный октаэдр построен исходя из аналитического направления обхода символов U→F→T→N (правая часть рисунка)

• 4. из 2 и 3 следует, что если в логическом октаэдре определен любой один объект (то есть, определены все связи этого объекта) и одна из всех связей остальных объектов – то мы можем определить, является ли это построение аналитическим или синтезирующим по отношению к исходному объекту.

Объекты и числовые плоскости. Симметрии.

Любое лингвистическое слово или группу слов мы будем называть объектом. Мы будем изображать объект в виде окружности или четырехугольника, внутри которого находится его название. Объект может находиться во взаимосвязи с другими объектами. Эти взаимосвязи мы будем называть связями или валентностями.

схематическое изображение четверичного обьекта, шаблон числовой плоскости, двуразрядная числовая плоскость

Они будут изображаться линиями, соединяющими объекты между собой. Каждой связи может быть сопоставлен символ, определяющий логическое отношение между связываемыми объектами в этом случае мы будем говорить о детерминированной' (локализованной) связи между объектами. В случае, если связи сопоставлено множество символов или символы, описывающие связь отсутствуют, то связь является индетерминированной (делокализованой). Если связь объекта не объединена с другим объектом то такую связь мы будем называть валентной связью, а количество необъединенных связей – валентностью. На рисунке представлен объект с четырьмя детерменированными валентными связями.

Числовые поверхности

Числовой плоскостью будем называть таблицу - квадратную матрицу, элементами которой является последовательность целых неотрицательных чисел. Порядок следования элементов в матрице определяется шаблоном числовой плоскости, простейший шаблон изображен на рисунке в центре. Рекурсивное (вложенное) применение данного шаблона образует числовую плоскость. Количество рекурсий (вложений), требуемое для образования числовой плоскости, будем называть глубиной рекурсии, уровнем фрактализации или разрядностью числовой поверхности. Например, на рисунке справа изображена числовая плоскость с разрядностью 2, она содержит 16 чисел от 0 до 15. Каждому десятичному числу на числовой плоскости будет соответствовать четверичное число, выраженное через символы, такие числа будем называть симметриями. Например, числу 14 будет соответствовать симметрия UF, а числу 9 симметрия FT. Заметим, что симметрии, состоящие из одного, многократно повторяющегося символа будут находиться в углах числовой плоскости произвольной разрядности. Это одна из особенностей числовой плоскости.

Существует важное отличие между арифметикой чисел по основанию 4 (или любому другому основанию) и арифметикой симметрий. В арифметике симметрий мы оперируем не абстрактными числами, выражающими только количество или порядок следования некоторых элементов, а логическими понятиями (симметриями), выражающими сложную, иерархическую симметрию какой-либо одной группы элементов, относительно другой группы элементов. Поэтому в арифметике симметрий реализуется более строгое отношение к ведущим нулям и разрядности симметрий, чем в арифметике чисел (в частности, по основанию 4). Например, одно и то же число 234 =023₄ =0023₄ имеет разный логический смысл, выражающийся как неравенство симметрий FU <> NFU <> NNFU. Анализ логического смысла симметрий, как абсолютного, так и по отношению друг к другу является одной из задач теории логики четырех состояний.

Проекции на числовые плоскости

логический "магический" модуль, поясняющий закон отрицания-отрицания.

Диаграммы объектов октаэдра на двухразрядной числовой плоскости

	ATTENTION! THIS IS THE FIRST SKETCHES! ARTICLE WILL BE COMPLETED!
	ВНИМАНИЕ! ЭТО ПЕРВЫЕ ШТРИХИ! СТАТЬЯ БУДЕТ ЗАВЕРШЕНА!

Построения

Метод построения логического октаэдра
а тут можно посмотреть абстрактные логические построения описываемые тремя символами T, F, U

коды коммутации

Рассмотрим некоторый объект, входящий в конструкцию из объектов. Этот объект имеет четыре связи с другими объектами, и все эти связи выражены одним из четырех символов: N, T, F, U.