Элементарная теория

	WARNING! NOT ENOUGH LOGIC CRYSTALLS!
	МАЛО ИНФОРМАЦИИ! СТАТЬЯ НУЖДАЕТСЯ В ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИИ!

Символы

Четверичная логика (логика четырех состояний) оперирует четырьмя состояниями, которые мы будем именовать символами:

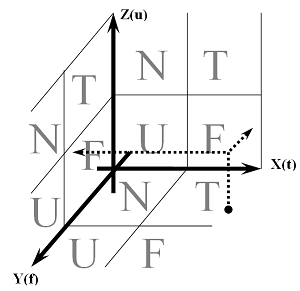
• T (от англ. “True” ) – означает состояние «Правда», геометрически ассоциируется с осью OХ, абсциссой. Имеет числовое значение 1.

• F (от англ. “False” ) - означает состояние «Ложь», геометрически ассоциируется с осью OY, ординатой. Имеет числовое значение 2.

• U (от англ. “Undefined” ) - означает состояние «Неопределенно», геометрически ассоциируется с осью OZ, аппликатой. Имеет числовое значение 3.

• N (от англ. “Null” ) - означает состояние «Вне понимания», геометрически это состояние ассоциируется с осью времени. Имеет числовое значение 0.

Таким образом, четыре состояния четверичной логики описываются набором из вышеуказанных символов. Этот набор мы будем называть "темным". Кроме темного набора символов, иногда, в редких случаях, мы будем пользоваться набором "светлых символов".

В четверичной логике светлые символы полностью эквиваленты темным символам, они отличаются небольшим смысловым различием, которое в настоящий момент не имеет значения, но которое может быть использовано в будущем, по мере развития идей логики. В общем и целом соответствующие светлые и темные символы совпадают.

Светлые символы:

• T (от англ. “Thesis” ) – тезис (ВЕРА_{(тавтология, манера-самотождественность μονή)}, ПРАВДА, ОСЬ OХ) (соответствует состоянию «Правда» формальной логики). Геометрически ассоциируется с осью OХ, абсциссой. Имеет числовое значение 1.

• A (от англ. “Antithesis” ) - антитезис (ОТРИЦАНИЕ_{(несокрытость ἀλήθεια)}, ЛОЖЬ, ОСЬ OY) (соответствует состоянию «Ложь» формальной логики). Геометрически ассоциируется с осью OY, ординатой. Имеет числовое значение 2.

• S (от англ. “Synthesis” ) - синтез (ПОНИМАНИЕ_{(выход за пределы, производство πρόοδος)}, НЕОПРЕДЕЛЕННОСТЬ, ОСЬ OZ) (соответствует уравнению формальной логики: TRUE OR FALSE == TRUE AND FALSE, где "OR" - операция слабой дизьюнкции, "AND" - операция коньюнкции, "==" - означает, что правая и левая части логического уравнения равны). В четверичной логике данное уравнение является отдельным символом S. При переходе от четверичной логики к формальной (формализация) мы будем пользоваться левой и только левой частью этого уравнения. Таким образом формально-логическое значение этого символа будет TRUE: (TRUE OR FALSE == TRUE). Геометрически ассоциируется с осью OZ, ординатой.Имеет числовое значение 3.

• N (от англ. “Nonsense” ) - нонсенс (РЕАЛИЗАЦИЯ_{(возвращение в свои границы, правильный выбор επιστροφή)}, ВНЕ_ПОНИМАНИЯ, ОСЬ ВРЕМЕНИ) (соответствует уравнению формальной логики: NOT(TRUE OR FALSE) == NOT(TRUE AND FALSE), где "OR", "AND", "==" - означает, то же что и в определении символа S - “Synthesis”(см. выше). Функция NOT() - означает формальнологическое отрицание. В четверичной логике данное выражение является отдельным символом N. При переходе от четверичной логики к формальной (формализация) мы будем пользоваться левой и только левой частью этого уравнения. Таким образом формально-логическое значение этого символа будет FALSE: (NOT (TRUE OR FALSE) == FALSE). Геометрически это состояние ассоциируется с осью времени. Имеет числовое значение 0.

По ряду причин при построении данной элементарной теории используются светлые символы. В дальнейшем, в более продвинутой части логики в основном используется темный набор символов.

Тезисы

Из определения символов и направлений их обхода возможно сформулировать два утверждения

утверждение А (запрет суперпозиции). Любой объект (логическое выражение) может находиться только в одном из 4-ех состояний по отношению к любому другому объекту:

• 1. данное выражение истинно (Т) (пример: белый цвет)
• 2. данное выражение ложно (A) (пример: черный цвет)
• 3. данное выражение неопределенно (S) (пример: серый цвет),
• 4. данное выражение бессмысленно, т.е. вне понимания (N) (пример: соленый цвет)

Указанные состояния являются дополняющими друг к другу и образуют полную группу состояний.

утверждение Б (направление обхода символов). Символы имеют прямой и обратный порядок следования.

Символы имеют прямой порядок следования N → T → A → S и обратный порядок следования S → A → T → N. Мы будем использовать прямой порядок следования символов для их нумерации: N=0 T=1 A=2 S=3 во всех наших построениях (хотя возможно создание теории с обратным порядком следования символов).

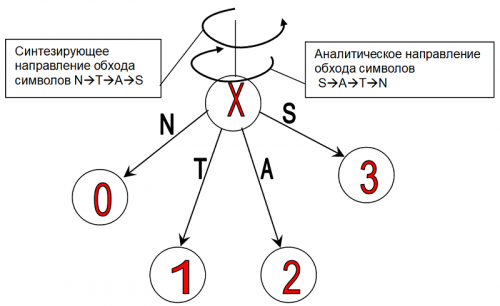
Мы можем использовать символы в качестве цифр и составлять из них числа в арифметике по основанию 4. Прямой порядок следования символов мы будем называть синтезирующим или индуктивным направлением обхода символов (0,1,2,3). Обратный порядок следования символов - будем называть аналитическим или дедуктивным направлением обхода символов (3,2,1,0).

Логическое построение

Возьмем в качестве исходного объекта X некоторое лингвистическое слово. Далее, возьмем некоторый другой, "второстепенный" объект Y - еще одно какое-то слово. Будем рассматривать отношение между объектом X и объектом Y, как если бы объект Y был свойством объекта X. Высказывание «объект Y присущ(свойственен) объекту Х»(*), в соответствии с запретом суперпозиции (утверждением А) может находиться только в одном из четырех (0,1,2,3) множеств эквивалентных между собой (относительно Х) объектов. Каждое такое множество мы также будем считать объектом. Отобразим это графически:

высказывание «объект Y присущ(свойственен) объекту Х»(*) может находиться в одном из множеств-объектов 0, 1, 2, 3.

Таким образом, высказывание (*) попадает в одно из множеств 0,1,2 либо 3. Обобщая наш пример, можно сказать, что абсолютно все слова, которые только можно вообразить объектом Y (свойством объекта X): Y₀,Y₁,…,Y_n, по отношению к объекту X можно распределить по множествам эквивалентностей 0,1,2,3.

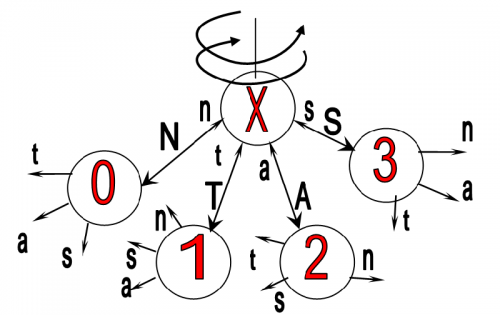
Рассуждая далее – мы можем сказать, что "0","1","2" и "3" - это четыре объекта, которые определяют собой объект Х, в символах логики четырех состояний N,T,A,S. Раз это так, то по аналогии с объектом Х - каждый из объектов 0,1,2 и 3 имеет свои четыре множества слов-объектов: множество N, множество T, множество A и множество S. Причем для каждого из множеств-объектов 0,1,2,3 определено уже одно множество объектов через объект Х.

В дальнейшем, любые рассматриваемые объекты и их возможные (несоединенные) и существующие (соединенные) логические связи мы будем называть логическим построением. Изображение на рисунке является логическим построением:

логическое построение.

В этом логическом построении объект X — станем называть эталонным объектом, а объекты 0,1,2,3 -- вспомогательными объектами. Можно предположить, что несоединенные связи n, t, a, s или, что тоже самое, множества свойств вспомогательных объектов 0, 1, 2, 3 связаны не только с эталонным объектом X, но и между собой.

Алгоритм сдвоенный логический октаэдр

Предлагается следующий алгоритм построения связей между вспомогательными объектами :

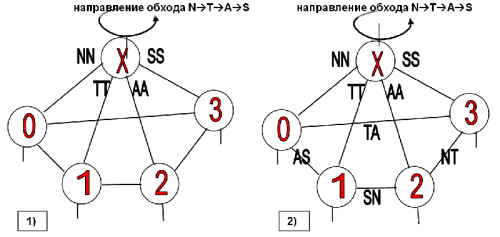
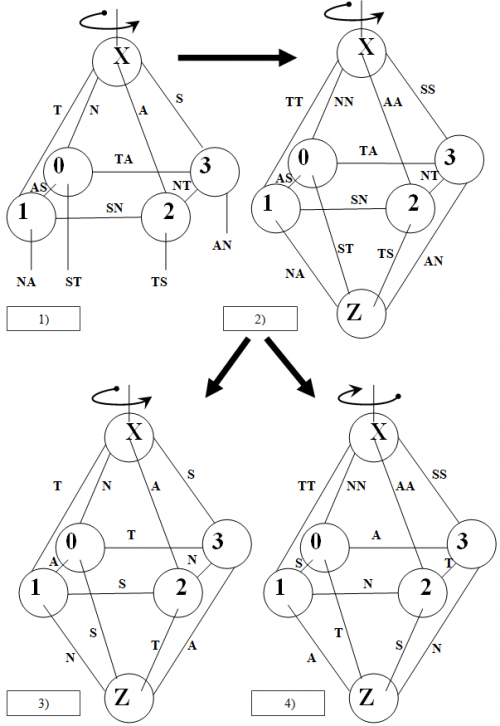
• 1. Соединим вспомогательные объекты между собой, как показано в части 1) нижнего рисунка.
• 2. Зададим порядок обхода символов (например, прямой порядок N→T→A→S)
• 2.1 Обговоренные ранее одиночные символы связи эталонного объекта со вспомогательными (n,t,a,s) запишем, для удобства дальнейших вычислений, в виде двух повторяющихся символов NN , TT, AA, SS. Эта тавтологическая замена (удвоение) необходима для разрешения неоднозначности выбора символов, возникающей далее
• 3. Определим значение связей 0—1, 1—2, 2—3 и 3—0 следующим образом:
• 3.1 Для каждой связи между вспомогательными объектами, в качестве возможных, остаются только два символа из четырех возможных.
• 3.2 Связь 0—1 можно описать символами A или S и только ими (так как символ N уже использован на построение связи 0—Х для объекта 0, а символ T уже использован на построение связи 1—Х для объекта 1).

Вопрос в том, какой символ брать первым, а какой вторым в двухсимвольной комбинации. Раз уж мы задали прямой порядок N→T→A→S, то для связи 0—1 мы будем указывать последовательность AS, а не SA. Потому что по заданному направлению обхода символов N→T→A→S сначала идет символ A, затем идет символ S, а не наоборот. Таким образом, связь 0-1 определена, как комбинация AS. Аналогично определим остальные связи между вспомогательными объектами. Это комбинации SN, NT и TA, соответственно для связей 1-2, 2-3, 3-0.

• 4. В результате получается построение, соответствующее части 2) рисунка

• 5. Вновь рассмотрим объекты 0,1,2 и 3 и определим последовательности (упорядоченные множества) символов (двухсимвольные комбинации), которые могут быть сопоставлены несоединенным связям 0—… , 1—… , 2—… и 3—… :
• 5.1. Для объекта 0, по первым символам двухсимвольных комбинаций всех других, уже определенных связей:

N, T, A – использованы. Остается свободным S.

• 5.2. Для объекта 0, по вторым символам комбинаций: N, A, S – использованы. Свободен T.
• 5.3. В итоге Связь 0—… определена, как ST
• 6. Аналогичным образом определим все несоединенные связи: 1—… , 2—… и 3—… . В результате получим их комбинации: NA,TS и AN, соответственно.
• 7. Объединим связи 0—… , 1—… , 2—… и 3—… . в объект Z, поскольку (и это важно) это возможно(!).
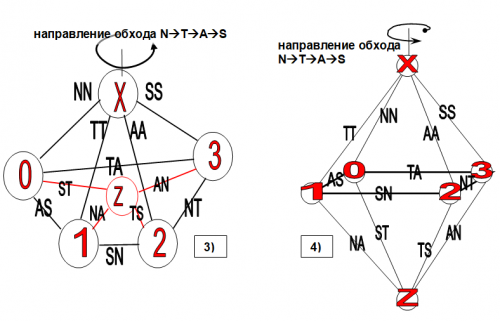
• 8. Объект Z полностью определен в терминах логики четырех состояний и называется 'результирующим объектом. Части 3) и 4) рисунка

октаэдр. 3) - плоское представление; 4) - трехмерное представление.

Результаты, выводы и определения

• 1. Полученное логическое построение является октаэдром. Октаэдр, распадается еще на 2 октаэдра. Связи первого, определяются по первому символу, а связи второго – по второму символу последовательности - двухсимвольной комбинации. Поэтому будем называть наше построение сдвоенным логическим октаэдром. Процесс, при котором определяется, каким из октаэдров является сдвоенный октаэдр, будем называть локализацией октаэдра.

алгоритм октаэдр. сдвоенный октаэдр и его локализации.

Локализацией в общем смысле будем называть процесс выбора логического символа из некоторого набора допустимых символов (комбинации символов) для соотнесения его со связью. Сдвоенный октаэдр будем также называть нелокализованным логическим октаэдром, а каждое из построений изображенных на рисунке выше – локализованным логическим октаэдром.

• 2. Отметим, что для построения локализованного октаэдра, необходимо задать 5 связей (например 4 связи исходного объекта X и одну из связей вспомогательных объектов). Если мы зададим только 4 связи, то получим нелокализованный октаэдр. Всего в октаэдре 12 связей.
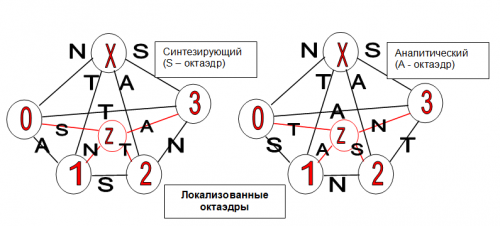
• 3. Сдвоенный октаэдр на рисунке построен исходя из синтезирующего направления обхода символов N→T→A→S (прямой порядок). При построении нелокализованного октаэдра, исходя из аналитического направления обхода S→A→T→N (обратный порядок), все символы в двухсимвольных комбинациях его связей поменяются местами. Воспользовавшись этим свойством, будем называть октаэдр, получающийся при локализации сдвоенного октаэдра по первым символам двухсимвольных комбинаций его связей:

A) синтезирующим октаэдром (S - октаэдром), при условии, что сдвоенный октаэдр построен исходя из синтезирующего направления обхода символов N→T→A→S (левая часть рисунка). B) аналитическим октаэдром (A - октаэдром), при условии, что сдвоенный октаэдр построен исходя из аналитического направления обхода символов S→A→T→N (правая часть рисунка)

• 4. из 2 и 3 следует, что если в логическом октаэдре определен любой один объект (то есть, определены все связи этого объекта) и одна из всех связей остальных объектов – то мы можем определить, является ли это построение аналитическим или синтезирующим по отношению к эталонному(исходному) объекту.

октаэдры

Карта Чисел

Числа в терминах логики четырех состояний

В соответствии с утверждением Б символы логики четырех состояний имеют порядок следования. Порядковые номера (начиная с 0) символов при синтезирующем направлении обхода символов (N→T→A→S), сопоставленные с самими символами станем называть цифровым представлением символов логики четырех состояний или цифрами логики четырех состояний. Как уже замечалось ранее, арифметика логики четырех состояний основывается на арифметике по основанию 4. Т.е. имеем всего 4 цифры: N(0), T(1), A(2), S(3). Привычная для нас арифметика – на арифметике по основанию 10 (всего 10 цифр: 0,1,2,3,4,5,6,7,8,9).

Число, записанное цифрами 0,1,2,3 станем называть, как это принято в математике, числом по основанию 4 или четверичным числом, а число, записанное символами четверичной логики (N, T, A, S) – симметрией. Запись четверичного числа (числа по основанию 4), как и симметрии, – тривиальна и однозначно переводится в число с другим основанием: Например, симметрия SAN переводится в четверичное число, а затем в десятичное следующим образом: SAN = 320₄ =(3*4² + 2*4¹ +0*4⁰) ₁₀ = (48+8+0) ₁₀ = 56₁₀ или SAN = 56₁₀ = (5*10¹ +6*10⁰)₁₀ (нижний индекс определяет основание системы счисления)

Существует важное отличие между арифметикой чисел по основанию 4 (или любому другому основанию) и арифметикой симметрий. В арифметике симметрий мы оперируем не абстрактными числами, выражающими только количество или порядок следования некоторых объектов, а логическими понятиями (симметриями), выражающими сложную, иерархическую симметрию какого-либо одного множества объектов, относительно другого. Поэтому в арифметике симметрий важно строгое отношение к ведущим нулям, иначе говоря, к разрядности симметрий, чем в арифметике обычных чисел (в частности, по основанию 4). Например, одно и то же число 23₄ =023₄ =0023₄ имеет одинаковый числовой, но разный логический смысл, выражающийся, как неравенство между разными симметриями: AS != NAS != NNAS. Анализ логического смысла симметрий (как абсолютного, так и по отношению друг к другу) является одной из задач логики четырех состояний.

Графическое представление четверичных чисел/симметрий.

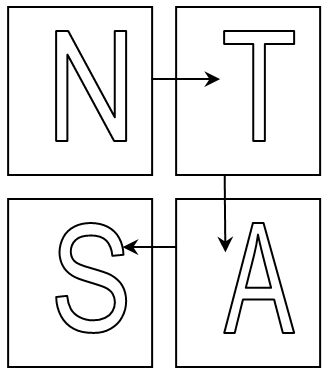
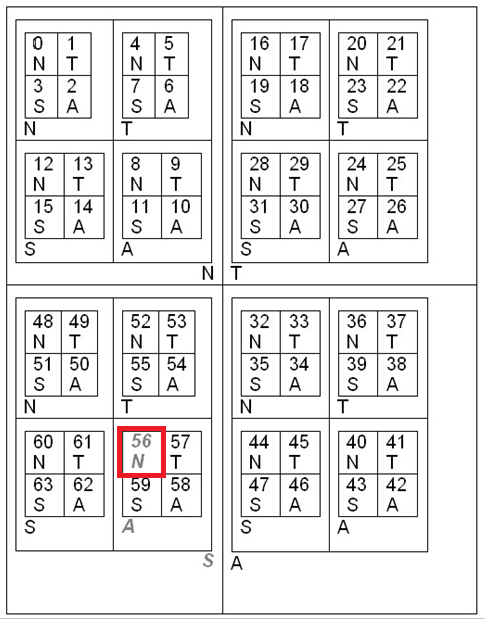
Графически симметрия представляется с помощью самоподобной "фрактальной" таблицы -- карты чисел. Вначале мы определяем таблицу 2 х 2 ячейки (рисунок А) в качестве шаблона("генератора фрактала"), который потом подставляется на место каждой ячейки этого же самого шаблона, причем эта операция производится такое число раз, какова разрядность симметрии минус 1.

рисунок А

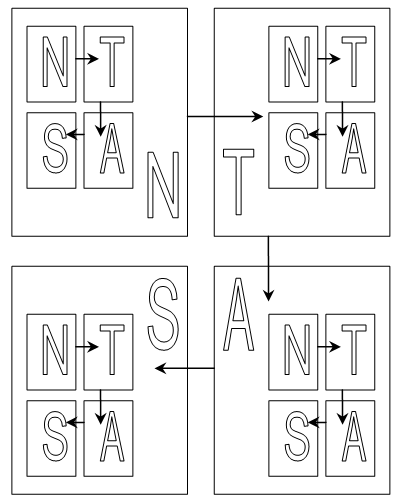
Таким образом, мы получаем таблицу n x n , где n – число цифр (разрядность) симметрии. Эту таблицу мы будем называть картой чисел, числовой плоскостью и в более общем случае – числовой поверхностью,

В элементарной теории мы будем рассматривать карты чисел, получающиеся из шаблона, который состоит из 4-ех квадрантов, соответствующих символам логики четырех состояний. Стрелками указано направление обхода символов. Шаблон – это всегда один разряд симметрии. Старшие числовые разряды симметрии находятся во внешних "сверхячейках" таблицы(квадрантах), младшие разряды, соответственно, находятся во все более внутренних квадрантах (рисунок Б).

рисунок Б

Таким образом, геометрически каждое число/симметрия изображается, как наименьший – наиболее внутренний квадрант карты чисел. То есть, как некая точка(наименьший квадрант) на плоскости (на "фрактальной" таблице). Например, набор цифровых (десятичных) представлений симметрий, записанный в квадрантах карты чисел показан на рисунке В. Цветом выделена точка (наименьший квадрант), соответствуюшая симметрии/числу SAN = 320₄ =(3*4² + 2*4¹ +0*4⁰) ₁₀ = (48+8+0) ₁₀ = 56₁₀.

рисунок В

На рисунке В изображена карта чисел разрядности 3.

Результаты, выводы и определения

• 1. Имеется возможность вычислять расстояния на карте чисел между двумя симметриями. Такие расстояния являются метриками карты чисел.
• 2. Симметрии с одинаковыми символами во всех разрядах сосредоточены в углах карты чисел. Такие симметрии будем называть когерентными.
• 3. Анализ симметрий следует проводить, в направлении от старшего разряда к младшему. Старшие разряды задают наиболее общие логические аспекты, младшие разряды – уточняют и детализируют эти аспекты.

В приложении приведен исходный код компьютерной программы на языке С++ для расчета карт чисел заданной разрядности:

Объекты и числовые плоскости. Симметрии.

	ATTENTION! THIS IS THE FIRST SKETCHES! ARTICLE WILL BE COMPLETED!
	ВНИМАНИЕ! ЭТО ПЕРВЫЕ ШТРИХИ! СТАТЬЯ БУДЕТ ЗАВЕРШЕНА!

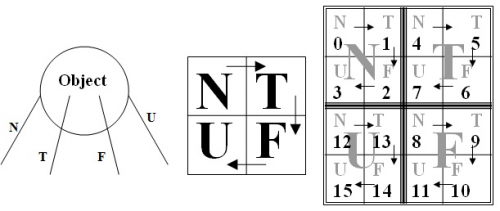
Любое лингвистическое слово или группу слов мы будем называть объектом. Мы будем изображать объект в виде окружности или четырехугольника, внутри которого находится его название. Объект может находиться во взаимосвязи с другими объектами. Эти взаимосвязи мы будем называть связями или валентностями.

схематическое изображение четверичного обьекта, шаблон числовой плоскости, двуразрядная числовая плоскость

Они будут изображаться линиями, соединяющими объекты между собой. Каждой связи может быть сопоставлен символ, определяющий логическое отношение между связываемыми объектами в этом случае мы будем говорить о детерминированной (локализованной) связи между объектами. В случае, если связи сопоставлено множество символов или символы, описывающие связь отсутствуют, то связь является индетерминированной (делокализованной). Если связь объекта не объединена с другим объектом то такую связь мы будем называть валентной связью, а количество необъединенных связей – валентностью. На рисунке представлен объект с четырьмя детерминированными валентными связями.

Числовые поверхности

	ATTENTION! THIS IS THE FIRST SKETCHES! ARTICLE WILL BE COMPLETED!
	ВНИМАНИЕ! ЭТО ПЕРВЫЕ ШТРИХИ! СТАТЬЯ БУДЕТ ЗАВЕРШЕНА!

Числовой плоскостью будем называть таблицу - квадратную матрицу, элементами которой является последовательность целых неотрицательных чисел. Порядок следования элементов в матрице определяется шаблоном числовой плоскости, простейший шаблон изображен на рисунке в центре. Рекурсивное (вложенное) применение данного шаблона образует числовую плоскость. Количество рекурсий (вложений), требуемое для образования числовой плоскости, будем называть глубиной рекурсии, уровнем фрактализации или разрядностью числовой поверхности. Например, на рисунке справа изображена числовая плоскость с разрядностью 2, она содержит 16 чисел от 0 до 15. Каждому десятичному числу на числовой плоскости будет соответствовать четверичное число, выраженное через символы, такие числа будем называть симметриями. Например, числу 14 будет соответствовать симметрия UF, а числу 9 симметрия FT. Заметим, что симметрии, состоящие из одного, многократно повторяющегося символа будут находиться в углах числовой плоскости произвольной разрядности. Это одна из особенностей числовой плоскости.

Таблица: карта чисел разрядности 3

0 N 1 T 3 U 2 F N 4 N 5 T 7 U 6 F T 12 N 13 T 15 U 14 F U 8 N 9 T 11 U 10 F F N	16 N 17 T 19 U 18 F N 20 N 21 T 23 U 22 F T 28 N 29 T 31 U 30 F U 24 N 25 T 27 U 26 F F T
48 N 49 T 51 U 50 F N 52 N 53 T 55 U 54 F T 60 N 61 T 63 U 62 F U 56 N 57 T 59 U 58 F F U	32 N 33 T 35 U 34 F N 36 N 37 T 39 U 38 F T 44 N 45 T 47 U 46 F U 40 N 41 T 43 U 42 F F F

Существует важное отличие между арифметикой чисел по основанию 4 (или любому другому основанию) и арифметикой симметрий. В арифметике симметрий мы оперируем не абстрактными числами, выражающими только количество или порядок следования некоторых элементов, а логическими понятиями (симметриями), выражающими сложную, иерархическую симметрию какой-либо одной группы элементов, относительно другой группы элементов. Поэтому в арифметике симметрий реализуется более строгое отношение к ведущим нулям и разрядности симметрий, чем в арифметике чисел (в частности, по основанию 4). Например, одно и то же число 234 =023₄ =0023₄ имеет разный логический смысл, выражающийся как неравенство симметрий FU <> NFU <> NNFU. Анализ логического смысла симметрий, как абсолютного, так и по отношению друг к другу является одной из задач теории логики четырех состояний.
подробнее можно посмотреть в галерее числовых плоскостей

Проекции на числовые плоскости

логический "магический" модуль. закон отрицания-отрицания.

Симметрии и октаэдр

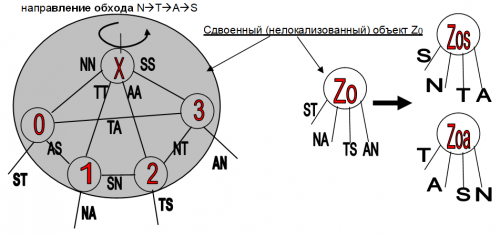
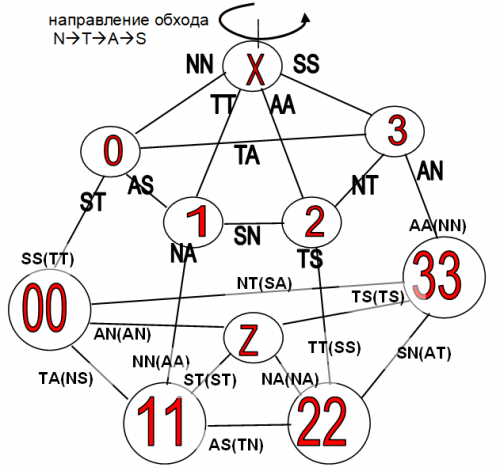
Вернемся к алгоритму октаэдр. При расчете по этому алгоритму мы получаем сдвоенный октаэдр (см. рис. А). На шаге 7 алгоритма мы создаем результирующий объект Z, как соединение несоединенных связей вспомогательных объектов. Уберем результирующий объект сдвоенного октаэдра. В этом случае сдвоенный октаэдр превращается в сдвоенный (нелокализованный) объект (Z0), который, по аналогии со сдвоенным октаэдром, распадается на синтезирующий (Z0s) и аналитический (Z0a) объект. Это также проиллюстрировано на рисунке.

рисунок А. Сдвоенный объект Z0, распадается на два

При локализации, сдвоенный объект превращается в обычный объект. Его можно использовать, как эталонный для построения еще одного сдвоенного октаэдра. Причем направление обхода (синтезирующее или аналитическое) нового сдвоенного октаэдра, уже будет определено на основании локализации сдвоенного объекта предыдущего сдвоенного октаэдра. Таким образом, можно создавать цепочки из локализованных октаэдров, а при хирургическом разъединении связей сразу нескольких объектов октаэдра -- создавать разнообразные пространственные логические сети -- меши. Пример логической цепочки из двух нелокализованных октаэдров изображен ниже, на рисунке.

рисунок Б

Вспомогательные объекты любого октаэдра в цепочке и их связи будем называть звеньями цепочки. Нумерацию звеньев, будем проводить от верхнего октаэдра к нижнему. Таким образом, объекты 0,1,2,3 – образуют звено 1, а объекты 00, 11,22, 33 – звено 2. Эталонный объект – является вырожденным случаем и представляет собой звено 0. Результирующий объект -– звено 3 -- и это также вырожденный случай.

Отсюда следует, что любой отдельно взятый октаэдр представляет собой цепочку из трех звеньев (звено 0, звено 1, звено 2), два из которых – звено 0 (эталонный объект) и звено 2 (результирующий объект) -- вырождены.

пояснения:

• не следует путать обозначения вспомогательных объектов (0,1,2,3,00,11,22,33) с числовым представлением символов логики четырех состояний N(0), T(1), A(2), S(3) или симметриями.
• Двухсимвольные комбинации в скобках записаны исходя из аналитического направления. Таким образом, они записаны в направлении, обратном двухсимвольным комбинациям вне скобок.

Анализ результатов и определения

Заметим, что:

• 1. Как видно из построения на рис.Б, значения связей результирующего объекта Z не зависят от локализации верхней сдвоенного октаэдра. Отсюда следует, что при увеличении длины цепочки, связи любого звена будут выражены максимум четырехсимвольной комбинацией. При этом выбор символа для каждой связи будет определяться только локализациями текущей и предыдущей нелокализованного октаэдра.

• 2. связи 00-11,11-22,22-33 и 33-00 вспомогательных объектов нижнего нелокализованного октаэдра могут принимать всю группу значений (N,T,A,S). Для определения этих связей необходима локализация обоих нелокализованных октаэдров.

• 3. Путь от эталонного объекта к результирующему объекту, можно выразить через симметрию (при условии локализации всех нелокализованных октаэдров цепочки). При этом старший разряд симметрии соответствует одной из связей эталонного объекта, а младший разряд – одной из связей результирующего объекта.

Под (логическим) путем мы подразумеваем расстояние между объектами, выраженное минимальным набором связей. Заметим также, что путь от эталонного объекта к результирующему объекту цепочки всегда проходит через вертикальные ребра октаэдров. 'Логической траекторией или логическим выводом – будем называть набор связей, соединяющий два объекта произвольным образом. Заметим, что если какой-либо участок траектории, связывающей эталонный объект с результирующим, проходит через связь между вспомогательными объектами одного октаэдра (например, через связь 00-11), то такая траектория не может быть путем.

Связь между двумя вспомогательными объектами одного октаэдра будем называть паразитной. Паразитные связи лежат на горизонтальных ребрах октаэдров.

Логический путь – является самой короткой, а значит и самой эффективной траекторией, связывающей два логических выражения: предпосылку (эталонный объект) и вывод (результирующий объект). Следовательно, для построения эффективных логических выводов необходимо, по возможности, исключать паразитные связи между вспомогательными объектами.

При построении кратчайшего логического вывода желательно обходить:

• 1. связи между понятиями, которые указывают на то, что предпосылка находится вне пределов рассмотрения (N) и понятиями, которые подтверждают достоверность предпосылки (T). Другими словами связь (0-1), вспомогательных объектов на рис. Б.
• 2. связи между понятиями, которые подтверждают достоверность предпосылки (T) и понятиями, которые устанавливают ложность этой предпосылки (A). Другими словами связь (1-2), вспомогательных объектов на рис. Б.
• 3. связи между понятиями, которые устанавливают ложность предпосылки (A) и понятиями, которые указывают на неопределенность этой предпосылки (S). Другими словами связь (2-3), вспомогательных объектов на рис. Б.
• 4. связи между понятиями, которые указывают на неопределенность предпосылки (S) и понятиями, которые указывают на то, что предпосылка находится вне пределов рассмотрения (N) или на то, как эта предпосылка реализована (N). Другими словами связь (3-0), вспомогательных объектов на рис. Б.

Иначе логический вывод увеличится, и не будет представлять собой логический путь.

Всегда существуют четыре логических пути, связывающих эталонный и результирующий объекты в цепочке.

Заметим также, что для построения длинных (сложных и обстоятельных) логических выводов необходимо пользоваться паразитными связями.

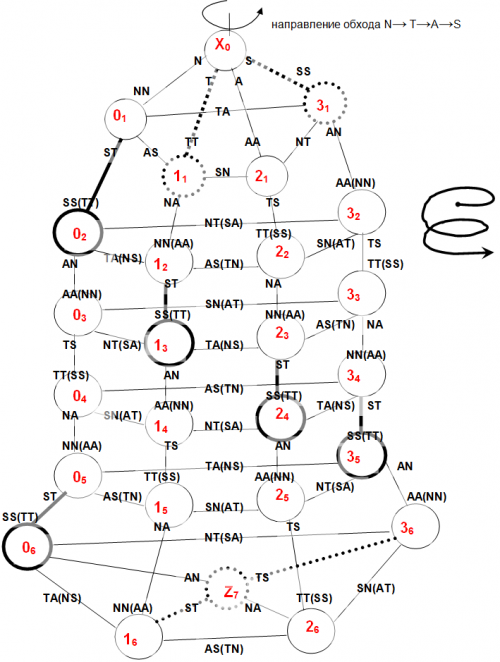
Цепочка нелокализованных октаэдров с большим количеством звеньев

Рассмотрим цепочку, изображенную на рис.12. В ней 8 звеньев. Напомним, что звенья 0 и 7 – являются вырожденными и представляют собой соответственно: эталонный и результирующий объекты. Заметим, что звено 6 полностью повторяет звено 2. Таким образом, при дальнейшем увеличении числа звеньев

рис.12 Цепочка из 8 звеньев (шесть нелокализованных бипирамид). Нижний индекс в обозначениях объектов указывает на звено, к которому относится объект.

мы получим многократное повторение фрагмента из звеньев со второго, по пятое. Заметим также, что звено 1 (первое звено) никогда не повторяется, какую бы длину не имела цепочка. То есть первое звено является уникальным звеном. Также следует отметить, что при локализации цепочки бипирамид первое звено перестает быть уникальным и многократно повторяется. Цепочки локализованных бипирамид будут рассмотрены в отдельной главе Первое звено и каждое из вырожденных звеньев цепочки нелокализованных бипирамид станем называть уникальными звеньями. То есть звеньями, которые не повторяются при увеличении длины цепочки

Явление многократного повторения некоторого фрагмента логического построения назовем свойством избыточности.

Логическое построение, объекты которого взаимосвязаны между собой и не имеют неспаренных связей, будем называть логически замкнутым построением. Логическое построение, в котором хотя бы один объект имеет, хотя бы одну неспаренную связь называется фрагментом.

Фрагмент из четырех последовательных и неуникальных звеньев станем называть полным фрагментом. Заметим, что каждое последующее звено в полном фрагменте, повернуто на один шаг (900) в соответствии с направлением обхода, заданном для эталонного объекта. Это проиллюстрировано на рис.12, на примере объектов, обведенных толстой линией. Пунктирной, толстой линией указано вырожденное продолжение этой тенденции для объектов в уникальных звеньях. Таким образом, все звенья цепочки повернуты относительно друг – друга и образуют спираль (спираль сдвига звеньев), направленную от эталонного объекта к результирующему объекту. Направление витков спирали соответствуют заданному в цепи синтезирующему направлению обхода.

Фрагмент, насчитывающий менее четырех последовательных и неуникальных звеньев, станем называть неполным фрагментом. Количество звеньев в неполном фрагменте будем называть остатком. Остаток может быть равен единице, двойке либо тройке. При отсутствии неполного фрагмента в построении – остаток равен нулю.

Фрагмент, насчитывающий более четырех последовательных и неуникальных звеньев цепи, назовем избыточным фрагментом. Заметим, что избыточный фрагмент может содержать в себе несколько полных фрагментов, либо несколько полных фрагментов и один неполный. То есть избыточный фрагмент может быть кратным либо некратным полному фрагменту. В общем случае кратностью мы будем называть количество полных фрагментов в избыточном, полном или неполном фрагменте цепи. В избыточном фрагменте кратность всегда больше либо равна 1. В полном фрагменте кратность всегда равна 1. В неполном фрагменте кратность всегда равна 0.

Набор уникальных звеньев ( [объект X], [звено 1], [объект Z]) будем называть уникальным фрагментом, а набор вырожденных звеньев ( [объект X], [объект Z]) будем называть вырожденным фрагментом. Таким образом, уникальный фрагмент состоит из вырожденного фрагмента и уникального звена 1. Все остальные фрагменты: полный фрагмент, неполный фрагмент и избыточный фрагмент - будем называть неуникальными фрагментами.

Таким образом, любой неуникальный фрагмент можно охарактеризовать, как фрагмент с кратностью K и остатком R. Где K – количество полных фрагментов, а R – количество звеньев неполного фрагмента. Например, неуникальный (избыточный) фрагмент цепи, изображенной на рис.12 является фрагментом с кратностью 1 и остатком 1.

Цепь бипирамид, состоящую только из одного полного и одного уникального фрагмента будем называть полной и неизбыточной. Такая цепь имеет 7 звеньев (с X0 по Z6) или, другими словами, 5 бипирамид.

Цепь, состоящую из уникального фрагмента и неполного фрагмента, будем называть неполной. Такая цепь имеет 4, 5 или 6 звеньев или от 2 до 4 бипирамид, включительно.

Цепь, состоящую из уникального фрагмента и избыточного фрагмента, будем называть избыточной. Она имеет более 7 звеньев или более 5 бипирамид. Такая цепь представлена на рис. 12.

Заметим, что цепь, состоящая только из уникального фрагмента, соответствует бипирамиде. Поэтому бипирамиду можно называть также уникальной цепью.

Только в уникальной цепи (бипирамиде) все звенья уникального фрагмента идут последовательно одно за другим и связаны между собой. Будем называть это свойство – свойством последовательности уникального фрагмента или свойством уникальности. Все цепи, кроме бипирамиды лишены этого свойства. В таких цепях последнее звено уникального фрагмента [объект Z] отделено от остальной своей части с помощью неуникального фрагмента. Заметим также, что увеличение количества звеньев в цепи может происходить только за счет увеличения количества звеньев в неуникальном фрагменте. Таким образом, только неуникальный фрагмент обладает свойством роста. Свойство роста и свойство уникальности являются взаимоисключающими свойствами. То есть, при увеличении количества звеньев в уникальной цепи (бипирамиде), она теряет свое свойство уникальности и приобретает свойство роста. По мере роста неуникального фрагмента он проходит три последовательные стадии: неполный фрагмент полный фрагмент  избыточный фрагмент. Заметим, что при переходе неуникального звена от полного фрагмента к избыточному фрагменту в построении появляется свойство избыточности.

Цепь, состоящую только из неуникального фрагмента, будем называть неуникальной цепью. В такой цепи связи последнего звена неуникального фрагмента соединены со связями первого звена этого же фрагмента. Геометрически, неуникальная цепь представляет собой тор. Неуникальная цепь, состоящая из одного полного фрагмента, изображена на рис.13. При этом нумерацию звеньев в неуникальной цепи будем проводить, начиная с номера 2. Этим мы подчеркиваем отсутствие уникального фрагмента в неуникальной цепи. В частности, отсутствие звена 0 (эталонного объекта) и звена 1. Отсутствие уникального фрагмента в цепи и, следовательно, отсутствие бипирамид в цепи нелокализованных бипирамид будем называть свойством нового качества цепи. Неуникальные цепи являются важной логической структурой. Более подробно неуникальные цепи и свойства цепей будут рассмотрены в отдельной главе.

Построения

Метод построения логического октаэдра
а тут можно посмотреть абстрактные логические построения описываемые тремя символами T, F, U

коды коммутации

Рассмотрим некоторый объект, входящий в конструкцию из объектов. Этот объект имеет четыре связи с другими объектами, и все эти связи выражены одним из четырех символов: N, T, F, U.